Hanapin ang y-intercept ng sumusunod na quadratic function.
a. y = -4x^2 -7x + 12
Kahit hindi i-solve ay malalaman na agad natin na ang y-intercept ay (0, 12).
Dahil ang value ng x ay 0, at ang value naman ng y ay 12, ang y-intercept ay (0,12)
b. f(x) = 2x^2 + 6x + 4
Kahit hindi i-solve, ang y-intercept ay (0, 4).
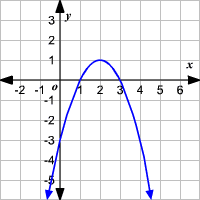
2. Ang x-intercept ng graph ng isang quadratic function ay (x,0). Maaaring isa o dalawa ang x-intercept ng graph ng isang quadratic function. Ang x-intercept ay ang point o points (value ng x at y) kung saan nasagi ng graph ang horizontal line o x-axis. Tingnan ang larawan sa itaas.
Ang x-intercept ng graph ng quadratic function f(x) = ax^2 + bx + c ay makukuha sa pamamagitan ng pag-solve ng quadratic function sa isang variable ===> ax^2 + bx + c = 0.
a. Isulat ang quadratic equation sa standard na porma (ax^2 + bx + c = 0)
Isulat sa standard na porma ng quadratic equation.
b. I-factor ang quadratic function bilang produkto (product) ng 2 linear factors. Ibig sabihin, ipa-factor natin ang (2x^2 + 6x + 4)
Kung mapapansin, ang mga real numbers na 2, 6, at 4 ay may common factor na 2,kung kaya't maaring isulat ang naunang equation sa ganito:
2x^2 +6x + 4 = 0 ===> 2(x^2 + 3x + 2) = 0
Ngayon, i-factor naman natin ang x^2 + 3x + 2. Paano?
Ano ang mga factors (dalawang numero na kung saan kapag minultiply mo silang dalawa ay lalabas ang naunang numero) ng x^2?
x at x ==> dahil kapag minultiply mo silang dalawa x (x) x and lalabas ay x^2
Ano ang mga factors ng 3x? 3 at x (pwedeng -3 at -x dahil ang product nila ay 3x din)
Ang 2? 2 at 1 (pwede ring -2 at -1 dahil ang product nila ay 2 rin)
======
Ano ang mga factors ng x^2 + 3x + 2?
Alam na natin na ang mga factors ng x^2 ay x at x, kung kaya:
( x +/- __) ( x +/- __) plus o minus ang nasa gita dahil hindi natin alam kung ano ang sign.
Ang blanko sa itaas ay ang mga factors ng c, na sa ating halimbawa ay 2. Ang maaari nating pagpilian ay 2 at 1 o kaya ay -2 at -1. Nguni't dapat nating alalahanin na ang dapat nating makuhang resulta kapag ito dinagdag (add) sa isa't isa ay 3. Kung gayon, anong mga factors ng 2 na kapag idinadagdag sa isa't isa ang magiging suma ay 3?
Kitang-kita naman na 2 at 1 dahil 2 + 1 ay 3. Kapag pinagsama mo ang iba pang factors ng 2, hindi na makukuha ang sumang 3.
Isulat ang nakuha nating factors ng x^2 + 3x + 2
(x + 2) (x + 1)
Isulat ang buong factors ng 2x^2 +6x + 4 = 0
2[(x + 2) ( x + 1) ] = 0
Upang tumama na zero ang equationg uto, dapat isa sa mga factors ay zero.
Ang unang factor na 2 ay hindi maaaring maging zero.
Equate natin sa zero ang ikalawang factor na x + 2 ==>
x + 2 = 0
x = -2
Kapag ang ikatlong factor na x + 1 naman ===>
x + 1 = 0
x = -1
Nangangahulugan na kapag ang x ay -2 o -1, magiging tama ang ating equation.
Subukin nating ilagay ang x = - 2 para maging tama ang nauna nating equation.
2x^2 + 6x + 4 = 0
2(-2)^2 + 6 )(-2) + 4 = 0
2(4) - 12 + 4 = 0
8 - 8 = 0 ====> tama ang x = - 2
Kung x = -1 naman.
2x^2 + 6x + 4 = 0
2(-1)^2 + 6(-1) + 4 = 0
2(1) - 6 + 4 = 0
2 - 2 = 0 ===> tama rin ang x = -1
Ang nakuha nating value na x ay -2 at -1. Dahil dito, may dalawa tayong x-intercepts. Ito ay ang mga points (puntos) na (-2, 0) at (-1, 0). Ito ay nangangahulugan na ang graph ng 2x^2 + 6x + 4 ay sumagi sa horizontal line (axis) o x-axis ng dalawang beses sa mga points na nabanggit.
SOLVING A QUADRATIC EQUATION using the QUADRATIC FORMULA
Isa ring pamamaraan ang pagresolba ng quadratic equation ay ang paggamit ng quadratic formula. Dahil dito dapat nating saulunin o tandaan ang pormulang ito dahil kalimitan ay hindi ito binibigay na "given" sa mga pagsusulit. Heto ang quadratic formula.
Ang solutions ng quadratic equation na ax^2 + bx + c = 0 ay
Magiging madali na ang paghanap ng value o values ng x kapag nasaulo natin ang quadratic formula.
Sa ating halimbawa sa itaas na 2x^2 + 6x + 4 = 0, gamitin natin ang quadratic dormula para hanapin ang mga katumbas ng x.
Dahil ang a = 2, b = 6, at c = 4 , heto ang kalalabasan:
x = - 6 +/- sqrt 6^2 - 4 (2)(4)
2(2)
x =
- 6 +/- sqrt 36 - 32
4
x =
- 6 +/- sqrt 4
4
x =
- 6 +/- 2
4
x =
- 6 + 2 at x =
- 6 - 2
4 4
x =
- 4 at x =
- 8
4 4
x = -1 at x = -2
Tama ang ating sagot. Kapareho ang value/s ng x kapag ginamit ang factoring method at quadratic formula. Kung tutuusin, mas madaling gamitin ang quadratic formula kung ating matatandaan na TAMA ang formula, maalam sa paggamit ng square root at babantayang mabuti ang mga SIGNS (positive + o negative -)
SOLVING QUADRATIC EQUATIONS by COMPLETING THE SQUARE
Isa pang paraan ng pagsagot sa mga quadratic equations ay ang Completing the Square. Basahin DITO ang pamamaraan.
Discriminant: Ang discriminant ng quadratic equation f(x) = ax^2 + bc + c ay
b^2 - 4ac
Pansinin na ang discriminant ang nakapaloob sa ating square root sa ating quadratic formula.
Sa ating halimbawa na 2x^2 + 6x + 4 = 0, ang discriminant ay :
b^2 - 4ac ===> 6^2 - 4(2)(4) = 36 - 32 = 4
Maraming malalamang impormasyon kapag nalaman natin kaagad ang discriminant.
a. Kapag ang discriminant ay
POSITIVE, ang graph ng quadratic equation ay may DALAWANG (2) x-intercepts (tulad ng ating halimbawa).
b. Kapag ang discriminant ay
ZERO , ang graph ng quadratic equation ay may ISANG (1) x-intercept.
c. Kapag ang discriminant ay
NEGATIVE, ang graph ng quadratic equation ay WALANG (0) x-intercepts at sa mga ganitong kaso;
i. Ang buong graph ay nasa ITAAS ng x-axis kapag ang value ng
a ay MAS MALAKI sa ZERO.
ii. Ang buong graph ay nasa IBABA ng x-axis kapag ang value ng
a ay MAS MALIIT sa ZERO o negative.
Vertex of Quadratic Function
Ang vertex ng quadratic function ay ang points (x,y) kung saan tumataas o bumababa ang graph ng isang quadratic equation. Ito ang pinakamataas o pinakamababang bahagi ng parabola. (Tingnan ang larawan sa itaas).
Mahalagang malaman ang vertex ng isang quadratic formula para malaman natin ang anyo nito o maiguhit ito sa x at y-axis.
Ipagpalagay na ang value ng x ay h at ang value ng y ay k. Ang h at k ang kalimitang ginagamit na simbolo sa mga libro sa pagkuha ng coordinates (x and y point) ng vertex.
Isa sa paraan ng pagkuha ng vertex ng parabola ay ang paggamit ng mga pormulang ito:
a. Para sa value ng x o h ===> h = -b/2a
b. Para sa valeu ng y o k ====> k =
(4ac - b^2)
4a
Subukin natin ang formula sa itaas sa ating halimbawa na 2x^2 + 6x + 4
Ang a = 2, b = 6, at c = 4
Para sa value ng x o h ==> h = -6/2(2) = -6/4 = -3/2 or -1 1/2
Para sa value ng y o k ==> k =
(4ac - b^2)
4a
k =
(4(2)(4) - 6^2) =
32 - 36 =
-4 = -1/2
4(2) 8 8
Kung gayon ang ating vertex (x,y or h,k) ay nasa puntos - 1 1/2 at -1/2
Saulunin lamang ang formula at magiging madali ang paghahanap ng values ng vertex.
Reference:
1.
http://www.purplemath.com
2.
http://www.drdelmath.com/