Lesson 6 - Solving Quadratic Equations in Taglish by Factoring, Completing the Square, and Using the Quadratic Formula

 Lesson 6 – Quadratic Equations

        Matapos nating mapag-aralan ang tungkol sa linear equations at ang kaugnayan ng mga ito sa pagresolba ng mga problema sa pang-araw-araw na buhay, dadako naman tayo sa quadratic equations.

Ang quadratic equation na may isang variable/unknown ay isang equation kung saan ang pinakamataas na exponent ng variable ay 2.

        Ang karaniwang anyo ng isang quadratic equation na may isang variable na kinakatawan ng x ay: 

        ax² + bx + c = 0 

kung saan ang a, b, at c ay mga constant at ang a ≠ 0.

Ang pinakakaraniwang ginagamit na paraan sa paglutas ng mga quadratic equation ay ang mga sumusunod:

Solving Quadratic Equations by Factoring

1. Ang factoring o pag-factor ay ang pinakamadaling paraan ng paglutas ng mga quadratic equation. Gayunpaman, nangangailangan ito ng kasanayan sa iba't ibang mga pamamaraan ng factoring. Bukod dito, hindi lahat ng quadratic equation ay malulutas sa pamamagitan ng factoring.

        Upang malutas ang isang quadratic equation sa pamamagitan ng factoring, sundin ang mga hakbang na ito:

        a. Ilipat ang lahat ng mga termino sa kaliwang bahagi ng equation upang ang kanang bahagi ay maging katumbas ng zero.

        b. Pasimplehin at i-factor ang quadratic expression na karaniwan na isang trinomial.

        c. Ang bawat isa sa mga factor ay isa na ngayong linear equation. I-equate ang bawat factor sa 0 at lutasin ang bawat linear equation para sa hinahanap na variable.

HALIMBAWA 1

        Solve for x in the equation 12x² - 9  = -10x + 3 

Step 1: Ilipat ang lahat ng terms sa kaliwang panig.

          12x²  - 9 = -10x + 3

  12x² – 9 + 10x - 3 = -10x + 3 + 10x - 3

      12x² +10x – 12 = 0

Step 2: Simplihen at i-factor

12x² + 10x – 12 = 0

6x² + 5x - 6 = 0 

(2x + 3) (3x – 2) = 0

Step 3: I-solve nang magkahiwalay ang dalawang factors.

2x + 3 = 0 at 3x – 2 = 0

      2x = -3       3x = 2

  2𝑥/2 = −3/2    3𝑥/3 = 2/3

𝑥 = −3/2         𝑥 = 2/3

Step 4: State your final answer.

There are two roots, namely −𝟑/𝟐   and 𝟐/𝟑.

Solving Quadratic Equations by Completing the Square

2. Ang completing the square ay ginagawa sa pamamagitan ng pagsunod sa mga hakbang na ito:

        a. Ilipat ang lahat ng constant term sa kanang bahagi ng equation.

        b. Hatiin o i-multiply ang magkabilang panig ng equation upang ang maging coefficient ng x² ay 1.

        c. Tukuyin ang constant na idaragdag sa kaliwang bahagi ng equation upang ito ay maging isang perpektong trinomial. Idagdag din ang constant na ito sa kanang panig ng equation. Ang constant na idaragdag ay ang square ng kalahati ng numerical coefficient ng linear term (bx).

        d. I-factor ang kaliwang bahagi ng equation.

        e. I-extract ang square root ng bawat panig ng equation. Ang square root ng kaliwang bahagi ng equation ay linear na ngayon at ito ay katumbas sa 

± square root sa kanang bahagi ng equation.

        f. Lutasin ang bawat isa sa mga linear na equation para makuha ang mga root.

HALIMBAWA 2

        Solve for x in the equation 3x² – 36x + 42 = 0.

Step 1: Ilipat ang constant sa kanang panig ng equation.

  3x² – 36x + 42 = 0

            3x² -36x = -42

Step 2: Hatiin o i-multiply ang equation upang maging 1 ang coefficient ng x². 

Sa ating problema, magagawa natin ito sa ating equation kung idi-divide natin ito ng 3.

            3x² -36x = -42

            x² – 12x = - 14

Step 3: Complete the square.

Paano ito gagawin?

Ang numerical coefficient ng linear term na -12x ay -12. Ang kalahati ng -12 ay -6 at ang square ng -6 ay 36.

Kaya ang constant na idaragdag sa magkabilang panig ng equation ay 36.

                        x² – 12x = - 14

 x² -12x + 36 = -14 + 36

x² – 12x + 36 = 22

Step 4: I-factor ang kaliwang panig ng equation.

x² – 12x + 36 = 22

(x – 6) (x – 6) = 22

(x – 6)² = 22

Step 5: Kunin ang square root ng bawat panig ng equation.

     (x – 6)² = 22

     

Step 6: Kunin ang value ng x.

   

Step 7: State your final answer.

The roots of the equation are 

Solving Quadratic Equations Using the Quadratic Formula

3. Maaaring gamitin ang quadratic formula upang malutas ang anumang quadratic equation.

        Sundin ang mga hakbang na ito sa paggamit ng quadratic equation.

        a. Ilipat ang lahat ng mga termino sa kaliwang bahagi ng equation upang ang kanang bahagi ay maging katumbas ng zero.

        b. Pasimplehin ang equation.

        c. Gamitin ang quadratic formula kung saan:

a = ang coefficient ng quadratic term (ax²); 

b = ang coefficient ng linear term (bx) ; at 

c = ang constant.

HALIMBAWA 3

Solve for h in the equation 3h² – 15h = -18

Step 1: Ilipat ang lahat ng termino sa kaliwang panig ng equation upang maging zero ang kanang panig.

3h² – 15h = -18

3h² – 15h + 18 = -18 + 18

3h² – 15h + 18 = 0

Step 2: Gawing simple ang equation.

3h² – 15h + 18 = 0

h² – 5h + 6 = 0

Step 3: Tukuyin ang value ng a, b, at c sa equation.

h² – 5h + 6 = 0

a = 1 b = -5 c = 6

Step 4: Kunin ang value (roots) ng h gamit ang quadratic formula.

Thus, the roots of our equation are 3 and 2.

Step 5: Optional. Check the answer.

For h = 3 

              3h² – 15h = -18   

3(3)² – 15(3) ≟ -18          

      3(9) – 45 ≟ -18               

        27 – 45 ≟ -18        

               -18 = -18              

For h = 2

            3h² – 15h = -18

      3(2)² – 15(2) ≟ -18

            3(4) – 30 ≟ -18

               12 – 30 ≟ -18

                      -18 = -18

REMEMBER

1 - A quadratic equation is an equation in which the highest power (exponent) of any of its variables is 2.

2 - The standard form of a quadratic equation with a single variable, x, is 

ax² + bx + c = 0where a, b, and c are constants and a ≠ 0.

3 – There are three ways in solving quadratic equations:  factoring, completing the square, and using the quadratic formula.

4 – You can only use the completing the square method as long as the coefficient of x² is 1.

5 – The formula for the quadratic equation is:

6 - When using the quadratic formula, you should be aware of three possibilities. These three possibilities are distinguished by a part of the formula called the discriminant. The discriminant is the value under the radical sign, b² – 4ac.

     A quadratic equation with real numbers as coefficients can have the following:

        a. Two different real roots if the discriminant b² – 4ac is a positive number                 (greater than zero).

        b. One real root if the discriminant b² – 4ac is equal to 0.

        c. No real root if the discriminant b² – 4ac is a negative number (less than                         zero).

--o0o--

Sanggunian: ALS Module: Equations 2

Lesson 5b - Solving Word Problems Using Two variables and Systems of Equations

 Lesson 5 – Applications of Linear Equations: Part 3

        Sa nakaraang aralin ay nai-apply natin ang ating natutunang konsepto at pamamaraan sa paglutas ng mga word problems na kinasasangkutan ng number, digit, uniform motion, money, age, investment, at mixture problems na may isang variable o unknown.

Sa bahaging ito ay pagtutunan naman natin ang pagsagot ng mga word problems gamit ang dalawang variables at/o dalawang equations.

Number Problems

        May mga word problems na nalulutas sa pamamagitan lamang ng isang variable o unknown at isang equation. Gayunpaman, may mga pagkakataon na mas madali ang pagsagot ng mga ito kung gagamit ng dalawang variables at dalawang sistema ng equations.

Tunghayan natin sa mga sumusunod na halimbawa:

HALIMBAWA 1

The sum of the two numbers is 17 and their difference is 7. Find the two numbers.

Let  x  =  the  smaller number

y = the larger number

Given: x + y = 17 (Equation 1)

y – x  = 7         (Equation 2)

Add the two equations.

x + y = 17

 + y – x = 7

           2y = 24

      y = 12

Substitute the value of y into either Equation 1 or 2 to find x.

    y - x = 7 (Equation 2)

         12 – x  = 7

          12 – 12 – x = 7 – 12

        -x = -5 

                  -1( -x = -5)

         x = 5

Check our answer.

        For Equation 1:

x + y = 17

        5 + 12 ≟ 17

      17 = 17

        For Equation 2:

y - x = 7

        12 - 5 ≟ 7

        7 = 7

        Thus, our smaller number is 5 and the larger number is 7.

REMEMBER

We can solve many problems by translating them into systems of equations and using the following problem-solving guidelines:

1.    Understand the problem. Read it carefully and decide which quantities are unknown. (Unawain ang problema. Basahin itong mabuti at magpasya kung aling mga quantities ang hindi alam o unknown.)

2.    Develop a plan. Represent one of the unknown values by one variable and the second unknown by another variable. (Bumuo ng isang plano. Katawanin ang isa sa mga unknown ng isang variable at ang pangalawa ng isa pang variable.)

3.    Carry out your plan. Study the stated facts until you understand their meanings. Then translate the related facts into equations in two variables. Solve the system of equations. (Isagawa ang iyong plano. Pag-aralan ang mga nakasaad na katotohanan hanggang sa maunawaan mo ang mga kahulugan nito. Pagkatapos ay isalin ang mga kaugnay na katotohanan sa mga equation sa dalawang variable. Lutasin ang sistema ng mga equation.)

4.    If available, check your answers using the derivations you made and not the given equation itself. Write a statement to answer the question being asked in the problem. (Kung mayroon, suriin ang iyong mga sagot gamit ang mga derivasyon na iyong ginawa at hindi ang ibinigay na equation mismo. Sumulat ng isang pahayag upang masagot ang tanong sa problema.)

Age Problems

HALIMBAWA 2

        Olive is 4 years younger than Popeye. Twenty years ago, Popeye’s age was 13 years more than half the age of Olive. How old are they now?

        Let    x    =    Olive's age now

                 y    =    Popeye's age now

Labis na makatutulong kung ilalagay natin sa isang table ang mga ibinigay na impormasyon.

        From the table, we can get a system of two equations in x and y.

        x = y – 4 (Equation 1)

y – 20 = ½(x – 20) + 13 (Equation 2)

Simplifying Equation 2, we will have:

y – 20 = ½(x – 20) + 13 (Equation 2)

y – 20 = 1/2x – 10 + 13

y – 20 = 1/2x + 3

y = 1/2x + 23         (Equation 3

        Substitute the value of x in Equation 1 into Equation 3.

        y = ½(y – 4) + 23         (Equation 3)

        y = 1/2y – 2 + 23

1/2y = 21

        2(1/2y = 21)

y = 42

Substitute 42 as the value of y in Equation 1 to find the value of x.

        x = y – 4 (Equation 1)

        x = 42 – 4

        x = 38

Thus, Olive is 38 years old and Popeye is 42 years old now.

        Check our answer.

For Equation 3:

   y = ½(y – 4) + 23 (Equation 3)

42 ≟ ½(42 – 4) + 23

42 ≟ ½(38) + 23

42 ≟ 19 + 23

42 = 42

For Equation 2: 

y – 20 = ½(x – 20) + 13

        42 – 20 ≟ ½(38 – 20) + 13

        22 ≟ 19 – 10 + 13

        22 = 22

     Since we got equality, our answer is correct.

Digit Problems

HALIMBAWA 3

In a three-digit number, the hundreds digit is twice the units digit. If 396 be subtracted from the number, the order of the digits will be reversed. Find the number if the sum of the digits is 17.

Let h = the hundreds digit

t =  the tens digit

u = the units digit

100h + 10t + u =  the number

h = 2u (Equation 1)

        h + t + u = 17     (Equation 2)

                       (100h + 10t + u) – 396 = 100u + 10t + h

100h + 10t + u – 396 -100u – 10t – h = 396

                                   99h – 99u = 396

                          99h/99 - 99u/99 = 396/99

                                           h – u = 4          (Equation 3)

Substitute h = 2u into Equation 3.

h – u = 4

         2u – u = 4

         u = 4

Substitute  4 as u into Equation 1.

h = 2u

h = 2(4)

h = 8

        Substitute u = 8 and h = 4 into Equation 2 to find the value of t.

h + t + u = 17

4 + t + 8 = 17

  4 – 4 + t 8 – 8 = 17 – 4 – 8

                       t = 5

Substitute these 3 values into our number.

100h + 10t + u =

100(8) + 10(5) + 4 = 

800 + 50 + 4  = 854

Thus, our number is 854.

Let us check our answer by substituting our values into our three equations.

For Equation 1:

h = 2u

8 ≟2 (4)

8 = 8

For Equation 2:

h + t + u = 17

      8 + 5 + 4 ≟ 17

         17 = 17 

For Equation 3:

h – u = 4

8 – 4 ≟  4 

       4 = 4

Since our left and right terms for our three equations are balanced, our answer is correct.

Mixture Problems

HALIMBAWA 4

Tikyo wants to make a 1000 ml of 50% alcohol solution mixing a quantity of a 20% alcohol solution with a 70% alcohol solution. What are the quantities of each of the two solutions he has to use?

        Let     x    =    amount of 20% alcohol

                  y    =    amount of 70% alcohol

Analyzing the problem, we find that two conditions must be met.

Condition 1

liters of 20% solution + liters of 70% solution = liters of 50% solution

x + y = 1000

        Condition 2

        pure alcohol in 20% solution + pure alcohol in 70% solution = pure alcohol in 50% solution

                        0.20x + 0.70y = 0.50(1000)

The system we must solve is:

       x + y = 1000      (Equation 1) 

 0.20x + 0.70y = 0.50(1000)      (Equation 2)

        Simplify Equation 2.

0.20x + 0.70y = 0.50(1000)

0.20x + 0.70y = 500

10(0.20x + 0.70y = 500)

2x + 7y = 5000 (Equation 3)

Multiply Equation 1 by 2.

x + y = 1000

2( x + y = 1000)

2x + 2y = 2000         (Equation 4)

Subtract Equation 4 from  Equation 3.

2x + 7y = 5000         (Equation 3)

    -     (2x + 2y = 2000)         (Equation 4)

            5y = 3000

         5y/5 = 3000/5

              y = 600

Substitute 600 as the value of y into Equation 1.

x + y = 1000

          x + 600 = 1000

        x + 600 – 600 = 1000 – 600

            x = 400

Thus, Tikyo has to use 400 liters of 20% alcohol and 600 liters of 70% alcohol to obtain 1000 liters of 50% alcohol.

        Let us check to confirm our answer.

          x + y = 1000      (Equation 1) 

400 + 600 ≟ 1000

          1000 = 1000

 0.20x + 0.70y = 0.50(1000)    (Equation 2)

      10(0.20x + 0.70y ≟ 500)

2x + 7y ≟ 5000

     2(400)x + 7(600) ≟ 5000

      800 + 4200 ≟ 5000

         5000 = 5000

Since we got equality in our original equations, our answer is correct.

Money Problems 

HALIMBAWA 5

The price of 3 chairs and 2 tables is ₱4500 and the price of 5 chairs and 3 tables is ₱7000. Find the price of 2 chairs and 2 tables.

Let  c =  the price of a chair

t = the price of a table

Given:

3c + 2t = 4500         (Equation 1)

5c + 3t = 7000         (Equation 2)

Subtract Equation 1 from Equation 2.

5c + 3t = 7000         (Equation 2)

  -   (3c + 2t = 4500) (Equation 1)

2c + t   =  2500

  2c – 2c + t = 2500 – 2c

          t = 2500 – 2c  (Equation 3)

Substitute Equation 3 into either Eq’n 1 or 2.

If Equation 2:

5c + 3t = 7000

  5c + 3(2500 – 2c) = 7000

5c + 7500 – 6c = 7000

  -c + 7500 – 7500 = 7000 – 7500

-c = -500

-1(-c = -500) 

                                c = 500

        Substitute 500 for c into Equation 3 to find t.

t = 2500 – 2c  (Equation 3)

t = 2500 – 2(500)

t = 2500 – 1000

t = 1500

Thus, the price of two chairs (2 x 500 = 1000) and two tables (2 x 1500 = 3000) is ₱ 4000 ( 1000 + 3000).

Let us check to confirm our answer.

                  3c + 2t = 4500 (Equation 1)

3(500) + 2(1500) ≟  4500

       1500 + 3000  ≟ 4500

                     4500 = 4500

                                 5c + 3t = 7000 (Equation 2)

5(500) + 3(1500) ≟ 7000

       2500 + 4500 ≟ 7000

                    7000 = 7000

        t = 2500 – 2c  (Equation 3)

1500 ≟ 2500 – 2(500)

1500 ≟ 2500 – 1000

1500 = 1500

Since we got equality in our original equations, our answer is correct.

Investment Problems 

HALIMBAWA 6

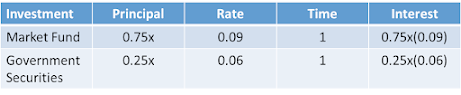
Bongbong invested ₱11,000.  Part of his money is invested in bonds which yield 8% and the remainder is invested in the money market which yields 10%.  His total annual income from these investments is ₱1,020.  Find the amount he has invested in each kind of investment.

Let      b     =  amount he invested in bonds at 8% 

                    m         = amount he invested in money market at 10%

                0.08b = annual income from 8% bonds investment

        0.10m =  annual income from 10% money market investment

b + m = 11000     (Equation 1)

       0.08b + 0.10m = 1020 (Equation 2)

        Multiply Equation 2 by 100.

0.08b + 0.10m = 1020         (Equation 2)

   100(0.08b + 0.10m = 1020)

          8b + 10m = 102000 (Equation 3)

        Multiply Equation 1 by 8.

b + m = 11000         (Equation 1)

8(b + m = 11000)

8b + 8m = 88000         (Equation 4)

Subtract Equation 4 from Equation 3.

         8b + 10m = 102000 (Equation 3)

     -   (8b + 8m = 88000) (Equation 4)

           2m = 14000

        2m/2 = 14000/2

             m = 7000

        Substitute 7000 as the value of m into Equation 1 to find b.

b + m = 11000         (Equation 1)

        b + 7000 = 11000

    b + 7000 – 7000 = 11000 – 7000

            b = 4000

Thus, Bongbong invested ₱4000 in bonds at 8% and ₱7000 in money market at 10%.

Let us check to confirm our answer.

b + m = 11000         (Equation 1)

          4000 + 7000 ≟ 11000

                  11000 = 11000

  0.08b + 0.10m = 1020         (Equation 2)

  100(0.08b + 0.10m ≟ 1020)

         8b + 10m ≟ 102000

 8(4000) + 10(7000) ≟ 102000

        32000 + 70000 ≟ 102000

             102000 = 102000

Since we got equality in our original equations, our answer is correct.

Motion Problems 

HALIMBAWA 7

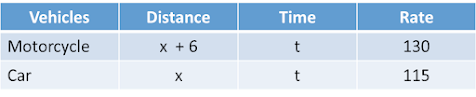
A boat can travel 16 miles up a river in 2 hours.  The same boat can travel 36 miles downstream in 3 hours.  What is the speed of the boat in still water?  What is the speed of the current?

Let  s =  speed of the boat in still water

                v = speed of the current

        Kung hindi pa bihasa sa ganitong klaseng problema, makatutulong nang malaki ang paggawa ng table upang ilagay ang ating mga datos.

    

        Mapapansin na ang rate (s + v) ng boat downstream ay ang speed nito sa kalmang tubig (still water) PLUS ang speed ng current  (o daloy ng tubig)  dahil mas mabilis ang takbo ng bangka kung paibaba o paayon sa daloy ng tubig.  Kung salungat naman sa daloy ng tubig o upstream, magiging mabagal ang takbo ng bangka kaya ibabawas natin ang speed ng current sa kanyang speed sa still water upang makuha ang rate (s - v) nito.

        Mula sa talahanayan o table, narito ang ating nakuhang equation:

16 = 2(s -  v) (Equation 1)

36 = 3(s + v) (Equation 2)

Divide Equation 1 by 2.

16 = 2(s - v) (Equation 1)

       16/2 = 2(s - v)/2

    8 = s - v (Equation 3)

Divide Equation 2 by 3.

36 = 3(s + v) (Equation 2)

       36/3 = 3(s + v)/3

12 = s + v (Equation 4)

        Add Equation 3 and Equation 4.

8 = s - v (Equation 3)

   +    12 = s + v (Equation 4)

         20 = 2s

     20/2 = 2s/2

        10 = s

Substitute 10 for s in any of the equations to find v. Let’s take Equation 4.

12 = s + v (Equation 4)

12 = 10 + v

12 – 10 = 10 – 10 + v

 2 = v

        Thus, the speed of the boat in still water is 10 miles per hour while the speed of the current is 2 miles per hour.

Let us check to confirm if our answer is correct.

16 = 2(s -  v) (Equation 1)

16 ≟ 2(10 – 2)

16 ≟ 2(8)

16 = 16

36 = 3(s + v) (Equation 2)

36 ≟ 3(10 + 2)

36 ≟ 3(12)

36 = 36

Since we got equality in our original equations, our answer is correct.

Pagsasanay 

Solve the following word problems and check your answers:

1.    If one number is three times as large as another number and the smaller number is increased by 19, the result is 6 less than twice the larger number. What is the larger number?

2.    A silver coin is 28 years older than a bronze coin. In 6 years, the silver coin will be twice as old as the bronze coin. Find the present age of each coin.

3.    The tens digit of a two-digit number is twice the units digit. If the digits are reversed, the new number is 36 less than the original number. Find the number.

4.    You need a 15% acid solution for a certain test, but your supplier only ships a 10% solution and a 30% solution. Rather than pay the hefty surcharge to have the supplier make a 15% solution, you decide to mix 10% solution with 30% solution, to make your own 15% solution. You need 10 liters of the 15% acid solution. How many liters of 10% solution and 30% solution should you use?

5.    The cost of admission to a popular music concert was ₱162 for 12 children and 3 adults. The admission was ₱122 for 8 children and 3 adults in another music concert. How much was the admission for each child and adult?

6.    Isko has invested in two savings accounts. One earns 10% and the other earns 15%. He invests ₱200 more in the account that earns 15%. The total interest earned for one year is ₱230. How much is invested in each account?

7.    A steamer goes downstream and covers the distance between two ports in 4 hrs., while it covers the same distance upstream in 5 hrs. If the speed of the stream is 2km/h, find the speed of the steamer in still water.

8.    The present ages of Bongbong and Sara are in the ratio 3:4. Five years from now, the ratio of their ages will be 4:5. Find their present ages.

Note: The above sample word problems were taken from different internet sites. 

ANSWERS:

Lesson 5a - Applications of Linear Equations in Word Problems: Uniform Motion, Investment, and Mixture Problems

  NOTES

1. This tutorial in Taglish is based on Module: Equations 2 prepared and published by the Department of Education of the Philippines for the Alternative Learning System (ALS) program.

2. Sorry for any typographical and/or grammatical error that has been missed.

3. Please comment for any incorrect answers.

Lesson 5 – Applications of Linear Equations: Part 2

        Sa nakaraang mga aralin ay nai-apply natin ang ating natutunang konsepto at pamamaraan sa paglutas ng mga word problems na kinasasangkutan ng linear equations na may kinalaman sa number, geometric, at work problems. Ang ating leksyon sa kasalukuyan ay nakapokus naman sa mga word problems na may kinalaman sa uniform motion, investment, at mixture problems.

Uniform Motion Problems

        Ang mga problemang may kinalaman sa distansya, d, oras, t, at uniform rate, r, ay tinatawag na mga uniform motion problems. Ang uniform motion ay isang paggalaw sa isang tuwid na linya na may pare-parehong bilis o velocity.

Ang mga problemang ito ay madalas na nililinaw sa pamamagitan ng paggawa ng sketch ng mga relasyon na kasangkot.

Sa ganitong mga klase ng word problem, dapat nating alalahanin ang ugnayan ng speed, time, at rate sa isa’t isa. Ito ay sa pamamagitan ng pagkuha ng isa sa kanilang mga formula.

        Karaniwan na nating naririnig ang salitang “80 km/hr” (80 kilometers per hour) na kumakatawan sa bilis (speed o rate (r)  ng isang sasakyan o bagay na gumagalaw. Ang 80 km ay kinakatawan ng distance (d) o distansyang tinakbo, ang hour naman ay ang time (t) o oras. Samakatuwid, ang rate = distance/time o r = d/t.

Mula sa pormulang ito ay makukuha rin natin ang relationship ng distance (d) sa time (t) at rate (r), gayundin ang time (t) sa distance (d) at rate (r). Gawin natin.

r = d/t ==> t(r = d/t) ==> rt = d or d = rt, ibig sabihin, ang distance (d) ay rate (r) multiply by time (t).

Mula sa d = rt ==> d/r = rt/r ==> d/r = t or t = d/r.

Ibig sabihin nito, ang time (t) ay distance (d) divided by rate (r).

        Isulat nating muli ang ating nakuhang pormula o relationship, kung saan ang

 r = rate, d = distance, at t = time. Kailangan natin ang kaalamang ito sa pagsagot ng uniform motion problems.

r = d/t

d = rt

t = d/r

Hindi kailangang saulunin lahat ang mga pormula. Isang pormula ay sapat na dahil makukuha natin ang iba pang pormula mula rito tulad nang ginawa natin sa nakaraang pahina.

HALIMBAWA 1

A policeman on a motorcycle is pursuing a car the speed of which is 115 kilometers per hour. The policeman is 6 km behind the car and is moving at a speed of 130 kilometers per hour. How long will it take the policeman to overtake the car?

I-sketch natin ang ating problema.

        Gumawa tayo ng table o talahanayan upang madaling malutas ang ating problema.

        Upang makumpara ang distansya ng dalawang sasakyan, dapat ay iisa ang starting point ng mga ito. Ang pinili kong starting point ay ang car na kakatawanin ng x. Ang motorcycle ay naging  x + 6, dahil ang pagitan nito sa car ay 6 km na.

Mamaya ay kukunin natin ang starting point ng motorcycle at ikumpara natin kung pareho ang ating magiging sagot.

        Distance traveled by motorcycle:

x + 6 = 130t

Isolate x:

x = 130t – 6 (Transposition)

Distance traveled by car:

x = 115t

Equate the two equations:

Since they have the same distance traveled as x.

          130t – 6 = 115t

        130t – 115t – 6 + 6 = 115t – 115t + 6  (Transposition)          15t = 6

            15t/15 = 6/15

                     t = 6/15

                     t = 2/5 (Simplification)

Thus, the motorcycle will catch up with the car after 2/5 of an hour or 24 minutes ==> ( 2/5 hr (60 min/hr) = 120/5 = 24 min.)

        Kung ang distance ng motorcycle ang ating magiging starting point, ganito na ang kalalabasan:

Distance traveled by motorcycle:

x = 130t

Distance traveled by car:

x – 6 = 115t

Kaya x – 6 dahil mas malayo na ng 6 km ang car mula sa motorcycle.

Isolate x:

x – 6 = 115t

      x = 115t + 6

Equate the two equations:

   130t = 115t + 6

130t – 115t = 115t – 115t + 6 (Transposition)

     15t = 6

        15t/15 = 6/15

         t = 6/15 or 2/5 or 24 minutes

Makikita na pareho lang ang ating nakuhang sagot.

HALIMBAWA 2

A car and a bus set out at 2 p.m. from the same point, headed in the same direction. The average speed of the car is 30 mph slower than twice the speed of the bus. In two hours, the car is 20 miles ahead of the bus. Find the rate of the car.

Illustrate the problem:

        Ilagay natin sa table ang ating mga given data:

        Distance traveled by car:

d + 20 = (2r – 30)2 (Equation 1)

Distance traveled by bus:

d = 2r (Equation 2)

        We can substitute Equation 2 into Equation 1 to find r.

     d + 20 = (2r – 30)2

     2r + 20 = (2r – 30)2

      2r + 20 = 4r – 60

      2r + 20 – 20 – 4r = 4r – 60 – 4r – 20

             -2r = -80

         -2r/-2 = -80/-2

                r = 40 mph ==> rate of bus

              2r – 30 = 2(40) – 30

                  = 80 - 30

                  = 50 mph ==> rate of car

Thus, the rate of the car is 50 mph.

        Let us check our answer by substituting our values into our original equations.

For Equation 1:

  d + 20 = (2r – 30)2

80 + 20 ≟ [2(40) – 30]2

80 + 20 ≟ (80 – 30)2

80 + 20 ≟ 100

       100 = 100

For Equation 2:

   d = 2r

80 ≟ 2(40)

80 = 80 

Since our left and right terms for our original equations are balanced, our answer is correct.

Investment Problems

        Ang ilang mga problema sa pamumuhunan ay gumagamit ng formula ng interes na I = PRT. Sa formula na ito, kinakatawan ng I ang interes, P, ang principal o halagang pinuhunan, R (%), ang rate ng interes at T, ang oras. Para sa mga layunin ng ating talakayan, dapat nating ipagpalagay na R ang taunang rate ng interes at ang T ay ibibigay sa mga taon (years).

Karamihan sa mga problema sa pamumuhunan ay nagsasangkot ng mga equation na may mga decimal coefficient. Ang nasabing equation ay maaaring malutas sa pamamagitan ng pagpaparami ng magkabilang panig ng equation sa pamamagitan ng power of 10 upang makakuha ng katumbas na equation na may mga whole number coefficients. 

HALIMBAWA 3

An investment counselor invested 75% of a client’s money into a 9% annual simple interest money market fund. The remainder was invested in 6% annual simple interest government securities. Find the amount invested in each if the total annual interest earned is ₱3300.

    Let x = total amount invested 

0.75x =  amount invested in the market fund

0.25x = amount invested in  government securities

        Gumawa tayo ng table para maging malinaw ang lahat.

        Set up our equation:

0.75x(0.09) + 0.25x(0.06) = 3300

                   .0675x + .015x = 3300

                       1000(.0825x = 3300)

                            825x/825 = 3300000/825

                                         x = ₱40000 ==> total amount invested

                  0.75x = 0.75(40000) = ₱30000 ==> invested in money  market

                 0.25x = 0.25(40000) = ₱10000 ==> invested in government  securities

        Substitute 40,000 as the value of x into the original equations to check if our answer is correct.

             0.75x(0.09) + 0.25x(0.06) = 3300

0.75(40,000)(0.09) + 0.25(40,000)(0.6) ≟ 3300

                                    2,700 + 600 ≟ 3300

                                               3,300 = 3300

Since we got equality, our answer is correct. 

HALIMBAWA 4

A man invests x pesos in bonds and ₱8000 more than this in stocks. How much did he invest in stocks if his total investment is ₱15000?

Let  x = investment in bonds

x + 8000 = investment in stocks

Our equation:

   x + x + 8000 = 15000

               2x + 8000 = 15000

   2x + 8000 – 8000 = 15000 – 8000

           2x = 7000

        2x/2 = 7000/2

             x = ₱3500 ==> invested in bonds

                x + 8000 = 3500 + 8000 = 11500

Thus, ₱11500 is invested in stocks.

Substitute 3500 as the value of x into our original equation to check if our answer is correct.

    x + x + 8000 = 15000

        3500 + 3500 + 8000 ≟ 15000

               15000 = 15000

Since we got equality, our answer is correct.

Mixture Problems 

        Ang isang paraan ng pagsusuri at paglutas ng mga mixture problems ay inilalarawan sa sumusunod na halimbawa.

HALIMBAWA 5

Tom and Jerry blended a chocolate mix that sells for ₱5 by mixing two types of chocolate. If they used 80 mL of chocolate that costs ₱6, how much of another chocolate costing ₱3 did they mix with the first?

    Let  x =  amount of ₱3 chocolate  mixed with ₱6 chocolate

        Kung hindi pa bihasa sa ganitong klaseng problema, makatutulong nang malaki ang paggawa ng table upang ilagay ang ating mga datos.

        Set up our equation:

          3x + 6(80) = 5(80 + x)

            3x + 480 = 400 + 5x

          3x + 480 – 5x – 480 = 400 + 5x – 5x – 480

                     -2x = - 80

                -2x/-2 = -80/2

                        x = 40

Thus 40 mL of chocolate @ ₱3 is needed for the mix.

        Ihalili natin ang 40 bilang value ng x sa ating orihinal na equation upang matiyak na tumpak ang ating sagot.

  3x + 6(80) = 5(80 + x)

     3(40) + 6(80) ≟ 5(80 + 40)

          120 + 480 ≟ 5(120)

             600 = 600

Dahil ang ating nakuha ay balanse, tumpak ang ating sagot.

HALIMBAWA 6

A chemist has 10 mL of a solution that contains 30% acid. How many mL of pure acid must be added to it in order to increase its acid content to 50%?

    Let  x  = amount of pure acid to be added

        Set up our equation:

(10 + x) (0.5) = 3 + x

         5 + 0.5x = 3 + x

   10(5 + 0.5x = 3 + x)

          50 + 5x = 30 + 10x

50 + 5x – 50 – 10x = 30 + 10x – 10x – 50

                 -5x = -20

            -5x/-5 = -20/-5

                    x = 4 

Thus, 4 ml of pure acid must be added to the solution to make its acid content 50%.

        Substitute 4 for x into our original equation to check if our answer is correct.

(10 + x) (0.5) = 3 + x

(10 + 4) (0.5) ≟ 3 + 4

          14(0.5) ≟ 7

                    7 = 7

Since we got equality, our answer is correct.

Pagsasanay 

        Solve the following word problems and check your answers:

1.    Kiko and Kikay start from the same point and jog in opposite directions. Kiko jogs 4 km/h faster than Kikay. After 3 hours, they are 30 kilometers apart. How fast did each jog?

2.    Bongbong leaves his house riding a bike at 20 km/h. Leni leaves 4 hours later on a motorcycle to catch up with him traveling at 60 km/h. How long will it take her to catch up with him?

3.     Manny invested ₱10,000, part at 6%, and the rest at 5%, in interest-bearing accounts. At the end of the year, his total investment income was ₱566. How much did Manny invest at each rate?

4.    An investment of ₱6,000 is made at an annual simple interest rate of 6%. How much additional money must be invested at an annual simple interest rate of 10% so that the total annual interest earned is 9% of the total investment?

5.    White sugar worth ₱70 per kilo is mixed with brown sugar worth ₱50 per kilo to obtain 50 kilos of a mixture worth ₱65 per kilo. How many kilos of each type is used?

6.    Solution A is 60% hydrochloric acid, while solution B is 85% hydrochloric acid. How many liters of each solution should be used to make 90 liters of a solution which is 75% hydrochloric acid?

ANSWERS:

Lesson 5 - Applications of Linear Equations: Number, Geometric, and Work Word Problems

 Lesson 5 – Applications of Linear Equations 

        Sa nakaraang mga aralin ay napag-aralan natin kunin ang solution set ng ating simultaneous equations o linear equations sa pamamagitan ng pag-plot ng graph ng mga ito, gamit ang  substitution method, at elimination method.  Sa leksyong ito, i-aaplay natin ang ating natutunang konsepto at pamamaraan sa paglutas ng mga word problems na kinasasangkutan ng linear equations.

MATUTO TAYO

        Ang kaalaman kung paano lutasin ang mga linear na equation ay maaaring gamitin sa mga sumusunod: number problems, geometric  problems, work problems, uniform motion problems, investment problems, at mixture problems na maaaring maging kapaki-pakinabang sa ating pang-araw-araw na buhay. Talakayin natin ang bawat uri ng word problem nang detalyado. Uunahin natin ang mga word problems na may kinalaman sa number, geometric figures, at work problems.

Number Problems

        Sa unang aralin ay nagawa nating isalin ang mga ordinaryong parirala at pangungusap sa matematika. Magagamit na natin ang kaalamang iyon upang malutas ang mga number problems. Tingnan ang mga sumusunod na halimbawa.

HALIMBAWA 1

If one number is three times as large as another number and the smaller number is increased by 19, the result is 6 less than twice the larger number. What is the larger number?

        Let x = the smaller number

3x = the larger number

x + 19 = the smaller number increased by 19

result = = (equal sign)

2(3x) – 6         = 6 less than twice the larger number

        Set up our equation and solve:

x + 19 = 2(3x) – 6

x + 19 = 6x – 6

      5x = 25 (Transposition)

   5x/5 = 25/5

        x = 5 ==>  the smaller number

      3x = 3(5) = 15 ==> the larger number

        Thus, 15 is the larger number.

        Ihalili natin ang ating nakuhang sagot sa ating orihinal na equation upang matiyak na tumpak ang ating sagot.

                x + 19 = 2(3x) – 6

                5 + 19 ≟ 2(15) - 6

                      24 ≟  30 - 6

                      24 = 24

        Dahil balanse ang ating nakuhang mathematical expressions, nangangahulugan ito na tumpak ang ating nakuhang sagot.

    

HALIMBAWA 2

Forty pesos less than  1/2  of Tim’s weekly salary is ₱800. How much does Tim earn each week?

    Let x = Tim’s weekly salary

    1/2x - 40 = Forty pesos less than ½ of  Tim’s weekly salary

is 800 = = 800

        Set up the equation and solve:

        1/2x – 40 = 800

                1/2x = 840 (Transposition)

            2(1/2x = 840)

                     x = 1680

Thus, Tim earns ₱1,680 per week.

        Ihalili natin ang ating nakuhang sagot na 1,680 bilang value ng x sa ating

orihinal na equation upang matiyak na tumpak ito.

                1/2x – 40 = 800

      1/2(1,680) - 40 ≟ 800

                 840 - 40 ≟  800

                         800 = 800

        Dahil balanse ang ating nakuhang mathematical expressions, nangangahulugan ito na tumpak ang ating nakuhang sagot.

Geometric Problems

        Ngayon, suriin ang isang problema na kinasasangkutan ng mga geometric figure.

HALIMBAWA 3

If the length of a rectangle is 5 m less than twice the width, and the perimeter is 44 m long, find its length and width.

Sa pagsagot ng ganitong klaseng problema, dapat ay alam natin ang hugis ng mga geometric figures at paano kukunin ang kanilang mga bahagi.

        Dahil kinapapalooban ng isang rectangle ang ating problema sa itaas, alalahanin natin ang pigura ng isang rectangle.

        Base sa larawan sa itaas, ang isang rectangle ay may apat na gilid. Dalawa ang mahabang sukat o tinatawag na length. Dalawa rin ang maikling gilid na tinatawag namang width. Ang mga length ay may parehong haba o sukat, gayundin ang mga width.

Dapat din nating alamin ang konsepto ng perimeter para masagot natin ang problema. 

        Ang perimeter ay ang kabuuang mga gilid ng isang  rectangle. Ito ay may pormulang:

Perimeter (P) = length + length + width + width or

P = 2 length + 2 width

Dahil batid na natin ang hugis, mga bahagi, at konsepto ng perimeter at rectangle, handa na nating sagutin ang ating word problem.

    Let x = width of the rectangle

2x – 5 = length of the rectangle

    44 = Perimeter of the rectangle

Gamit ang pormula ng perimeter na:

P = 2 length + 2 width, ihalili natin ang ating mga expressions.

                P = 2 length + 2 width

44 = 2(2x – 5) + 2x

44 = 4x – 10 + 2x

6x – 10 = 44                (Transposition)

6x = 54

6x/6 = 54/6

x = 9 m ==> width of the rectangle

2x – 5 ==> 2(9) – 5 ==> 18 – 5  =

13 m ==> length of the rectangle

        Thus, the length of our rectangle is 13 m and its width is 9 m.

Ihalili natin ang ating nakuhang mga sagot  sa pormula ng perimeter upang matiyak na tama ito.

   P = 2 length + 2 width

44 ≟ 2(13) + 2 (9)

44 ≟ 26 + 18

44 = 44

        Dahil tama ang nakuha nating equality, tumpak ang nakuha nating sukat ng length na 13 m at width na 9 m.

HALIMBAWA 4

The first side of a triangle is 5 cm less than its second side, the third side is 3 cm more than the first and the perimeter of the triangle is 17 cm long. How long is each side?

`     Let x = length of the 2nd side

  x – 5 = length of the 1st side

 (x – 5) + 3 = length of the 3rd side

     17 = perimeter of the triangle

        Set up the equation and solve:

side 1 + side 2 + side 3 = Perimeter of a triangle

        (x - 5) + x + [(x - 5) + 3] = 17

                     3x – 7 = 17 (Simplification)

                           3x = 24 (Transposition)

                        3x/x = 24/3

                             x = 8 cm ==> length of the 2nd side

                      x – 5 ==> 8 – 5 = 3 cm ==> length of the 1st side

       (x - 5) + 3 ==> 8 – 5 + 3 =  6 cm ==> length of the 3rd side

        Thus, the sides of our triangle measure 8, 3, and 6 cm.

Ihalili natin ang ating mga sagot sa pormula ng perimeter upang matiyak na tama ang mga ito.

side 1 + side 2 + side 3 = Perimeter of a triangle

   8 + 3 + 6 ≟ 17

      17 = 17

        Maaari rin nating ihalili ang 8 na value ng x sa ating original na equation.

            (x - 5) + x + [(x - 5) + 3] = 17    

            (8 - 5) + 8 + [(8 - 5) + 3] ≟ 17

                            3 + 8 + (3 + 3) ≟ 17

                                     3 + 8 + 6 ≟ 17

                                                17 = 17

    

        Dahil tama ang nakuha nating equality, tumpak ang nakuha nating sukat ng mga sides ng triangle na  3, 8, at 6 cm.

Work Problems

Sa paglutas ng mga work problems, tandaan na kung ang isang tao ay makakagawa ng isang trabaho sa loob ng 5 araw, nakukumpleto niya ang 1/5 ng trabaho sa isang araw, 2/5 sa dalawang araw, at x/5 sa x na araw. Nakakatulong ang isang diagram na ipakita ang relasyong ito.

 Complete Job

                                        1/5 ng trabaho ang matatapos sa isang araw.

        Sa pangkalahatan, kung aabutin ng b araw upang makumpleto ang isang trabaho, ang bahagi ng trabaho na maaaring gawin sa a na mga araw ay kinakatawan ng fraction na 𝒂/𝒃.

HALIMBAWA 5

Alfred can mow the lawn in 40 minutes and Abel can mow the lawn in 60 minutes. How long will it take for them to mow the lawn together?

        Let     x     = the number of minutes it will take the two men to complete the job together

𝑥/40     = the part of the job that Alfred can do in x minutes

𝑥/60     = the part of the job that Abel can do in x minutes

The relationship used in setting up the equation is:

Part of job done by Alfred + Part of job done by Abel = Complete job.

        That is: 𝑥/40 + 𝑥/60=1

        Multiply the equation with the LCM of 40 and 60 which is 120.

        120(𝑥/40 + 𝑥/60 = 1)

   120𝑥/40 + 120𝑥/60 = 120 

         3x + 2x = 120

                             5x = 120  

                                  5x/5 = 120/5

                                x = 24 minutes

Thus, the time taken for both of them to mow the lawn together is 24 minutes.

        Ihalili natin ang 24 minutes bilang value ng x sa ating orihinal na equation upang matiyak na tumpak ang ating sagot.

        𝑥/40 + 𝑥/60 = 1 

            24/40 + 24/60 ≟ 1 

    120(24/40 + 24/60 ≟ 1)

            3(24) + 2(24) ≟ 120

     72 + 48 ≟ 120 

           120 = 120

Since we got equality, thus, our answer of 24 minutes is correct.

HALIMBAWA 6

A swimming club manager needs to fill the pool in 8 hours and she knows that the built-in water line will take 12 hours to fill the pool. How many hours would it take the auxiliary hose to fill the pool with water?

    Let x = number of hours would it take the auxiliary hose to fill  the pool completely

    8/𝑥 = part of the auxiliary hose to fill the pool in 8 hours

    8/12 = part of the built-in water line to fill the pool in 8 hours

            Set up the equation and solve.

        8/𝑥 + 8/12 = 1

12x(8/𝑥 + 8/12 = 1)

     96x/𝑥  +  96𝑥/12 = 12𝑥 

                           96 + 8x = 12x

 96 – 96 + 8x – 12x = 12x – 12 – 96    (Transposition)

                 -4x = -96

            -4x/-4 = -96/-4

                    x = 24 hours

Thus, the auxiliary hose needs a minimum rate of 24 hours to fill the pool.

Substitute 24 as the value of x in the original equations to check if our answer is correct.

        8/𝑥 + 8/12 = 1

    

     8/24 + 8/12 ≟ 1

                24(8/24 + 8/12 ≟ 1)

     192/24 + 192/12 = 24 

                             8 + 16 = 24

                   24 = 24

Since we got equality, our answer of 24 hours is correct. 

Pagsasanay 

        Solve the following word problems and check your answers:

1. One number exceeds another number by 5. If the sum of the two numbers is 39, find the smaller number.

2. The denominator of a fraction exceeds the numerator by 4. If 6 is added to the numerator and 2 is subtracted from the denominator, the resulting fraction equals 5. Find the original fraction.

3. A rectangle is 4 times as long as it is wide. If the length is increased by 4 inches and the width is decreased by 1 inch, the area will be 60 square inches. What were the dimensions of the original rectangle?

4. It takes Marie 10 hours to pick sixty bushels of apples. Kyle can pick the same amount in 12 hours. How long will it take if they work together? Round your answer to the nearest hundredths.

ANSWERS: